什么是纠删码
纠删码(erasure coding,EC)是一种数据保护方法,它将数据分割成片段,把冗余数据块扩展、编码,并将其存储在不同的位置,比如磁盘、存储节点或者其它地理位置(来自百度百科)。最早是在通信行业解决部分数据在传输中损耗的问题,它的基本原理是把传输的信号分段,加入一定的校验再让各段间发生一定的联系,即使在传输过程中丢失掉部分信号,接收端仍然能通过算法把完整的信息计算出来。
目前,纠删码技术在分布式存储系统中的应用主要有三类:
- 阵列纠删码(Array Code: RAID5、RAID6等)
- RS(Reed-Solomon)里德-所罗门类纠删码
- LDPC(LowDensity Parity Check Code)低密度奇偶校验纠删码
磁盘阵列RAID
RAID0
RAID0 是一种非常简单的的方式,它将多块磁盘组合在一起形成一个大容量的存储。当我们要写数据的时候,会将数据分为N份,以独立的方式实现N块磁盘的读写,那么这N份数据会同时并发的写到磁盘中,因此执行性能非常的高。
但RAID0的问题是,它并不提供数据校验或冗余备份,因此一旦某块磁盘损坏了,数据就直接丢失,无法恢复了。因此RAID0就不可能用于高要求的业务中,但可以用在对可靠性要求不高,对读写性能要求高的场景中。
RAID1
RAID1 是磁盘阵列中单位成本最高的一种方式。因为它的原理是在往磁盘写数据的时候,将同一份数据无差别的写两份到磁盘,分别写到工作磁盘和镜像磁盘,那么它的实际空间使用率只有50%了,两块磁盘当做一块用,这是一种比较昂贵的方案。
RAID1其实与RAID0效果刚好相反。RAID1 这种写双份的做法,就给数据做了一个冗余备份。这样的话,任何一块磁盘损坏了,都可以再基于另外一块磁盘去恢复数据,数据的可靠性非常强,但性能就没那么好了。
RAID3
将数据按照RAID0的形式,分成多份同时写入多块磁盘,但是还会另外再留出一块磁盘用于写「奇偶校验码」。例如总共有N+1块磁盘,那么就会让其中额度N块用来并发的写数据,第N+1块磁盘用记录校验码数据。一旦某一块磁盘坏掉了,就可以利用其它的N块磁盘去恢复数据。
但是由于第N+1块磁盘是校验码磁盘,因此有任何数据的写入都会要去更新这块磁盘,导致这块磁盘的读写是最频繁的,也就非常的容易损坏。
RAID5
RAID5的方式可以说是对RAID3进行了改进。
RAID5模式中,不再需要用单独的磁盘写校验码了。它把校验码信息分布到各个磁盘上。例如,总共有N块磁盘,那么会将要写入的数据分成N份,并发的写入到N块磁盘中,同时还将数据的校验码信息也写入到这N块磁盘中(数据与对应的校验码信息必须得分开存储在不同的磁盘上)。一旦某一块磁盘损坏了,就可以用剩下的数据和对应的奇偶校验码信息去恢复损坏的数据。
RAID5校验位算法原理:$P = D1 \oplus D2 \oplus D3 … \oplus Dn$ (D1,D2,D3 … Dn为数据块,P为校验,$\oplus$为异或运算),因此最少需要3块,才有恢复能力,允许最多同时坏一块磁盘。
RAID6
RAID6除了每块磁盘上都有同级数据XOR校验区以外,还有针对每个数据块的XOR校验区,这样的话,相当于每个数据块有两个校验保护措施,因此数据的冗余性更高了。允许最多同时坏二块磁盘
Reed-Solomon
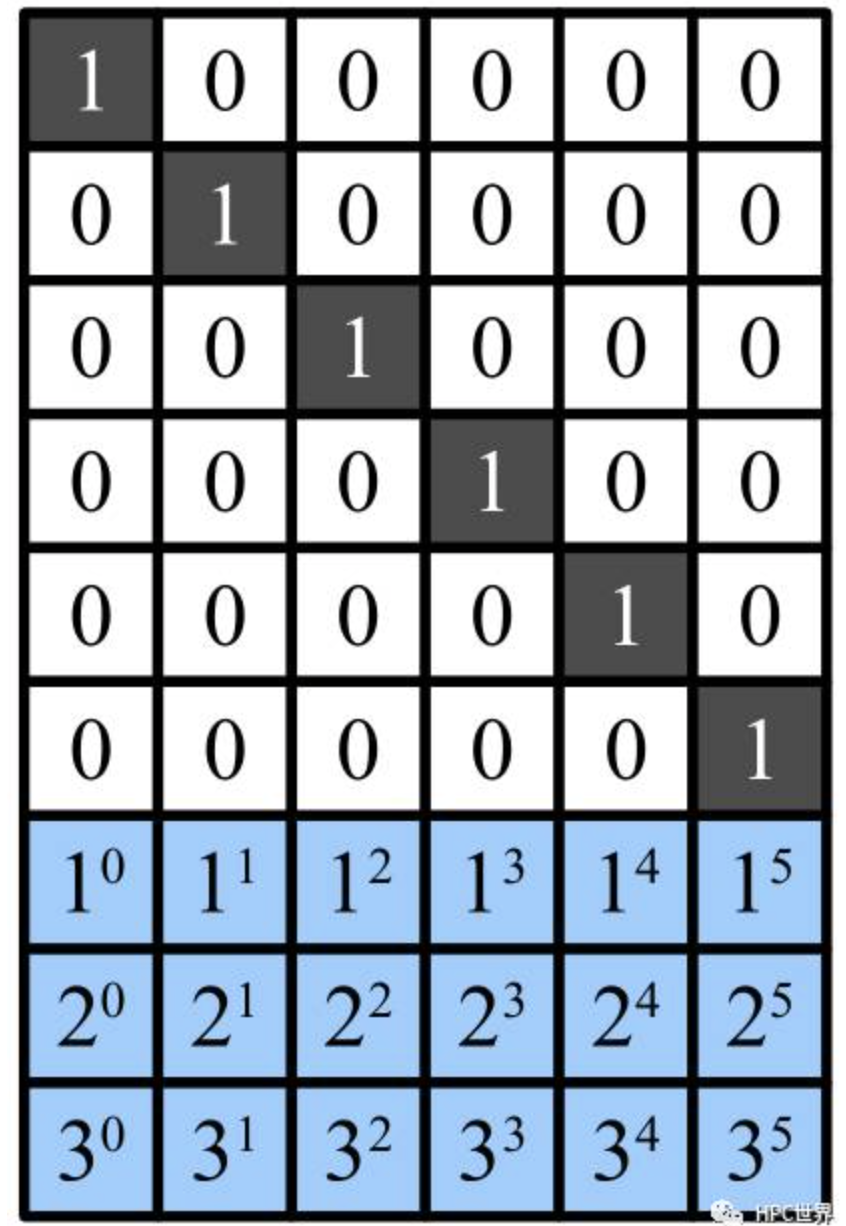
冗余级别为5+3的纠删码为例说明。将n个源数据块D1~Dn按列排成向量D,再构造一个(n+m)n矩阵B),B称为分布矩阵。对矩阵B有一个要求:它的任意n个行向量都是相互独立的,即这n个行向量组成的n*n矩阵可逆。矩阵B的前n行是单位矩阵I
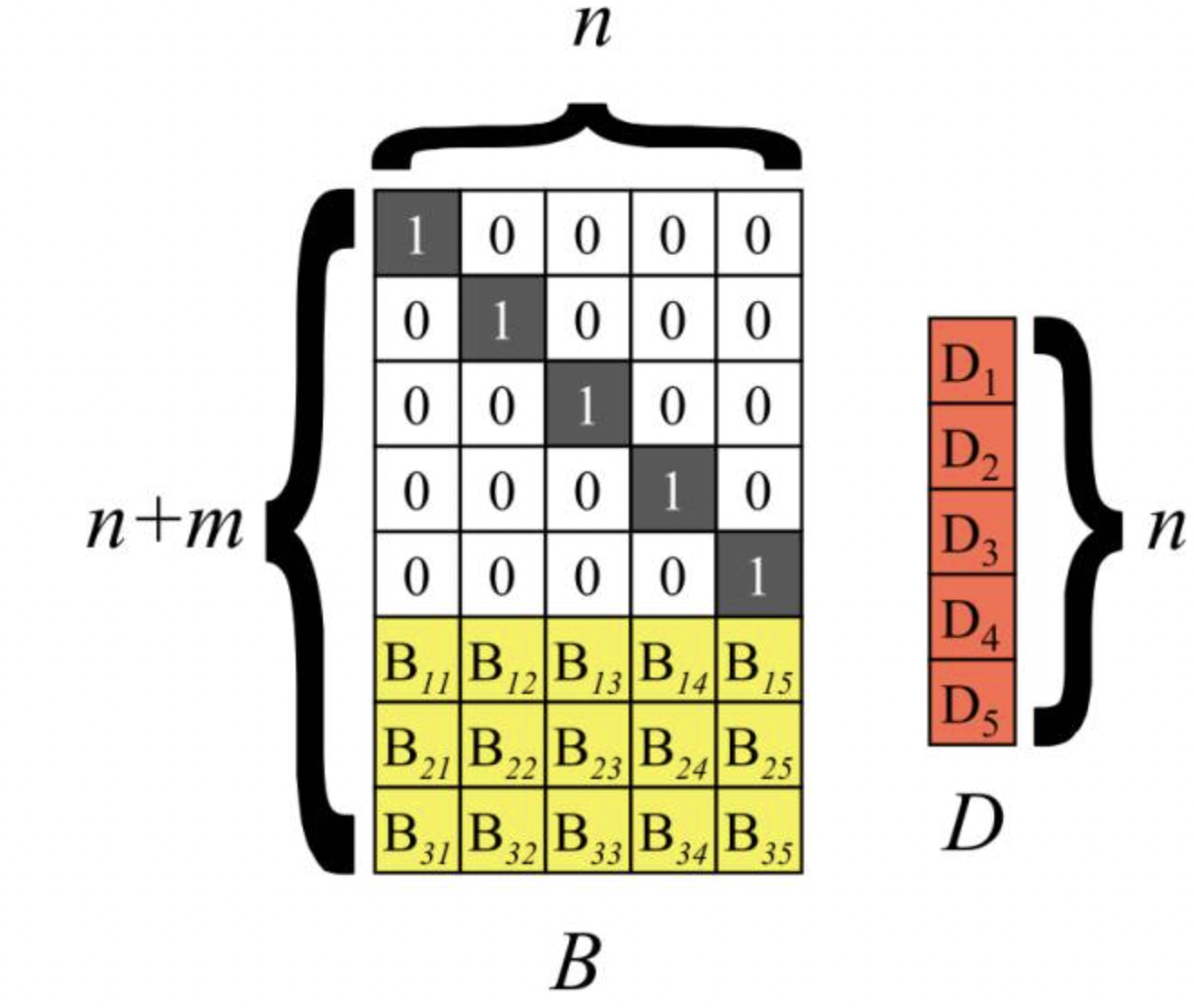
执行矩阵向量乘B*D,得到m个校验块C1~ Cm
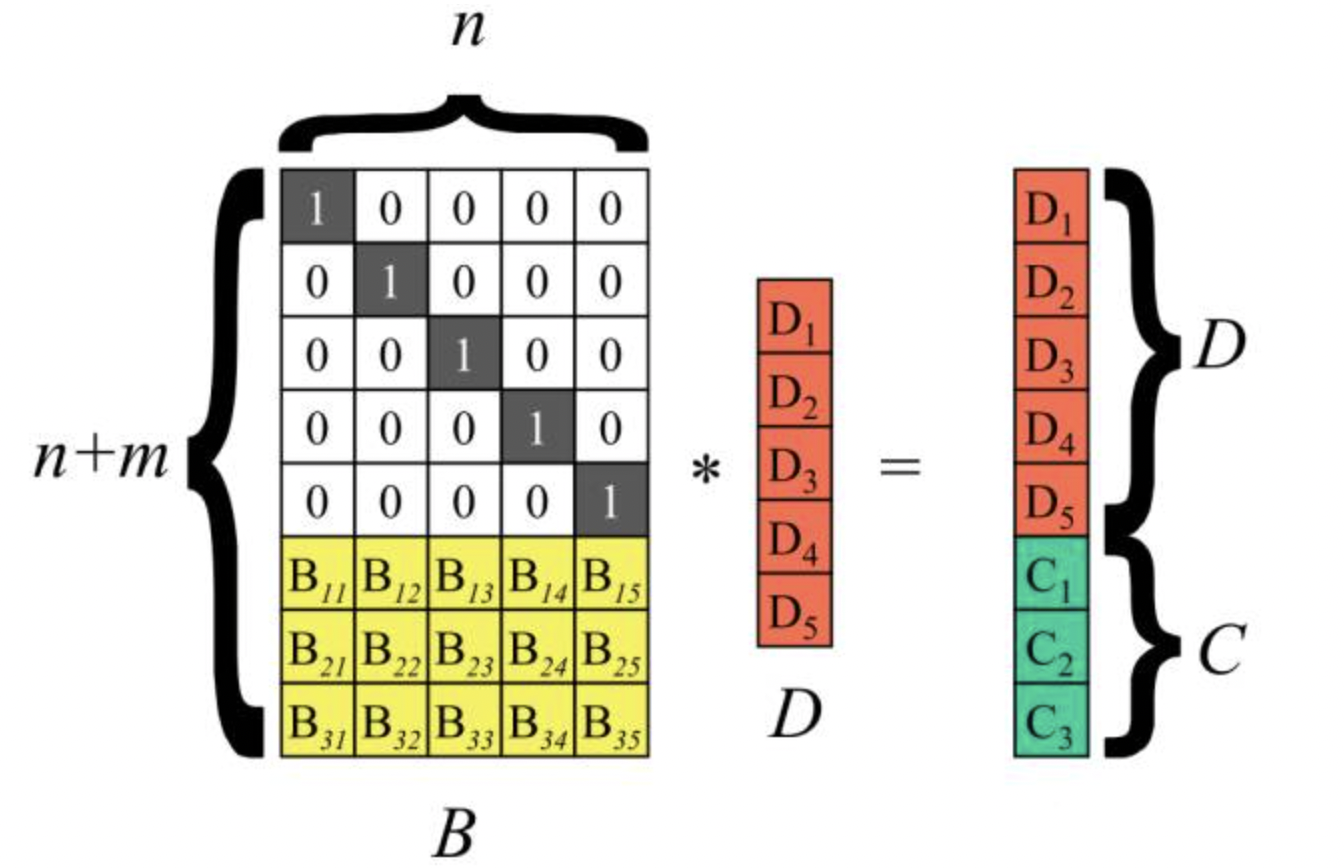
假设m个硬盘发生了故障,即图4中的数据块D1、D4、C2丢失,需要从剩下的n个数据块中恢复出来源数据D1~Dn。
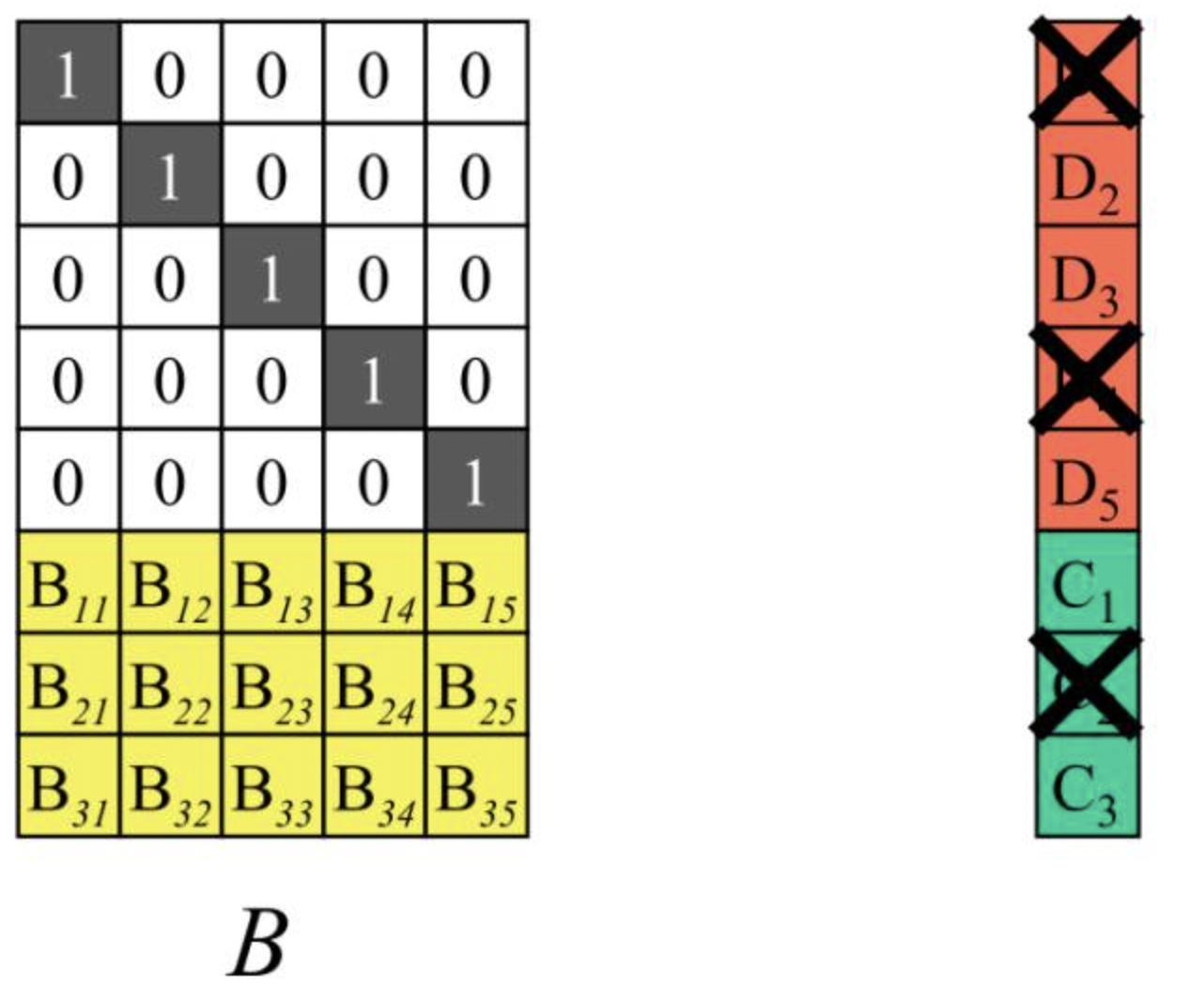
从矩阵B中将剩余数据块对应的行向量挑出来,组成新矩阵B’,B’乘以向量D的结果恰好是未故障的数据块
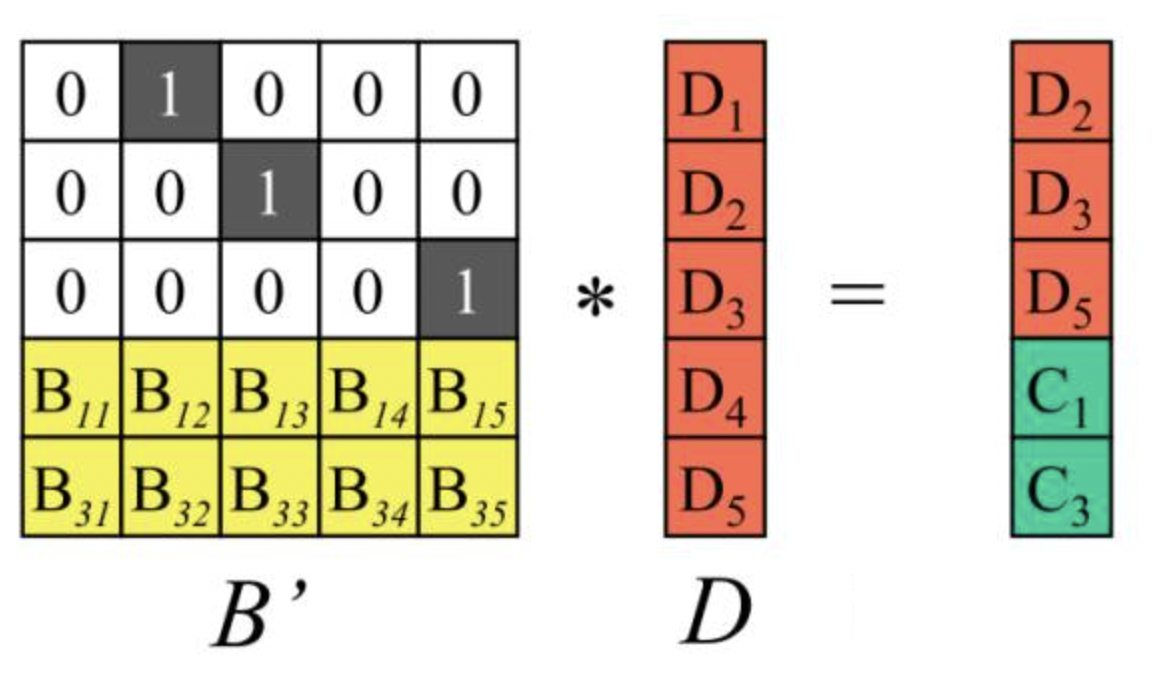
因为B的任意n行组成的矩阵都可逆,所以矩阵B’存在逆矩阵,记为${B’}^{-1}$,显然有${B’}^{-1}B’$=I。
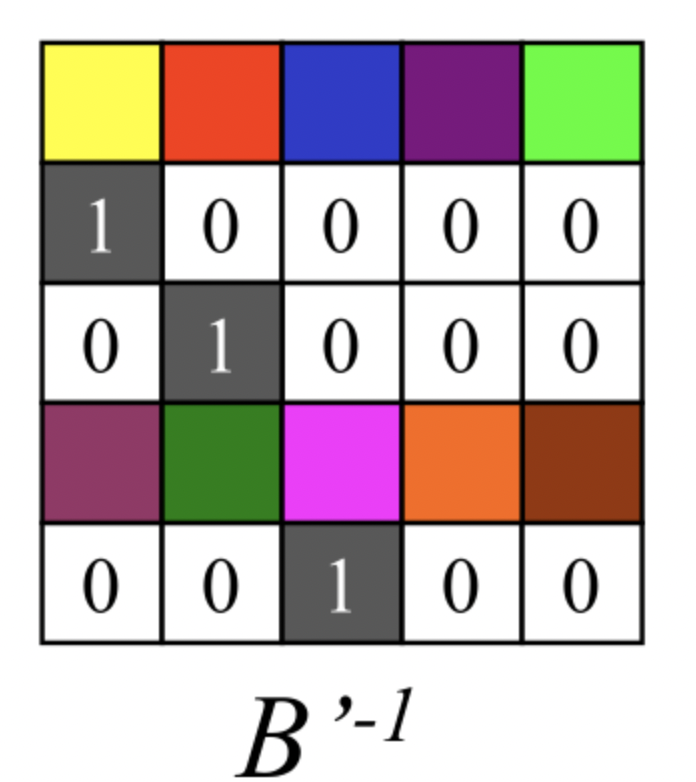
将图中等式的左右两边同时左乘矩阵${B’}^{-1}$,就得到了n个源数据块D1~Dn,完成数据恢复。
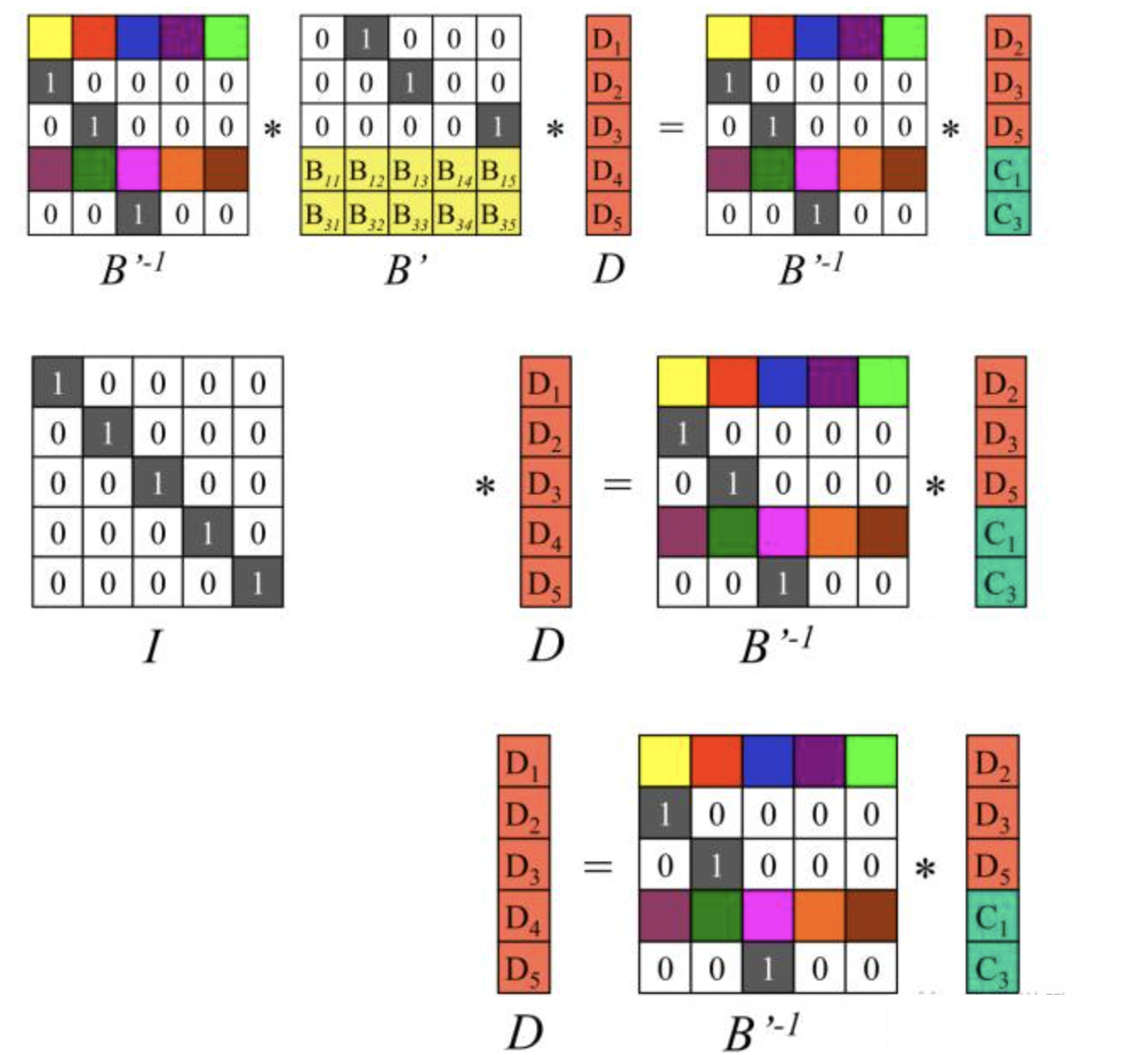
分布矩阵B的构造方式有很多种,这里介绍一种常用方法。
由线性代数知道,对互不相等的实数a1,a2,…,ak(k≥n),矩阵V的任意n行组成的矩阵都可逆。

从Vandermonde矩阵V中取出m行,用做分布矩阵B的下部m行,恰好满足对B的要求:任意n行都相互独立。例如冗余级别为6+3纠删码的分布矩阵B可以采用如下形式。