数据结构——树
1 树
树是由n个节点构成的有限集,其中当n=0时,称为空树。并且树恰好有n-1条边。
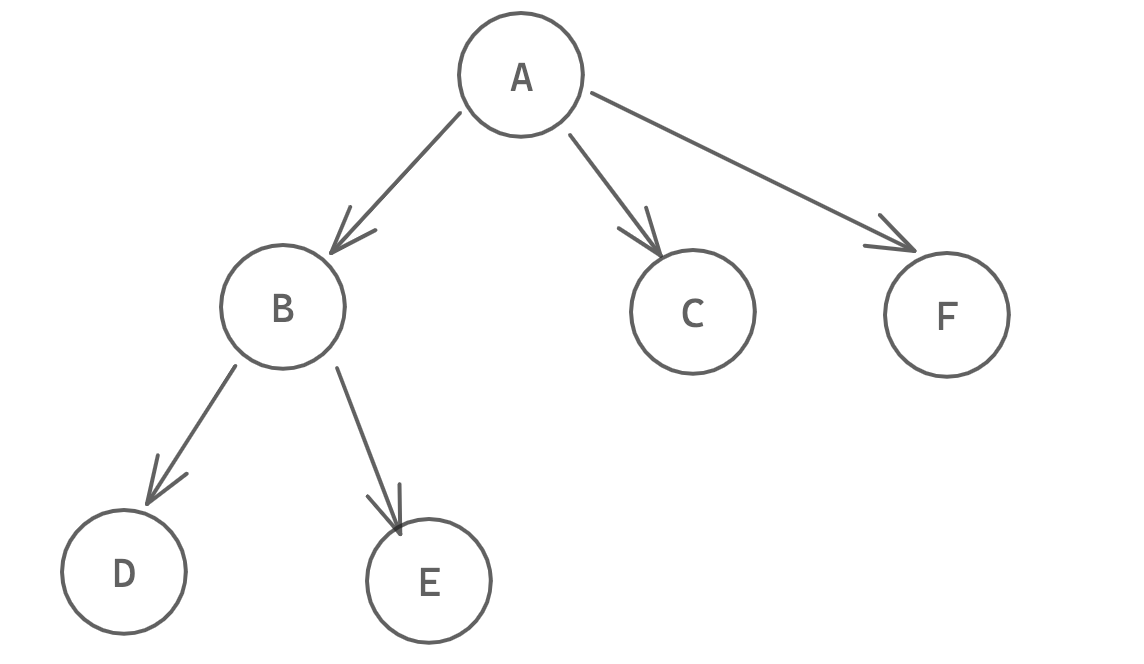
其中A是树的根
2 二叉树
顾名思义,二叉树就是一个节点只有两个子节点
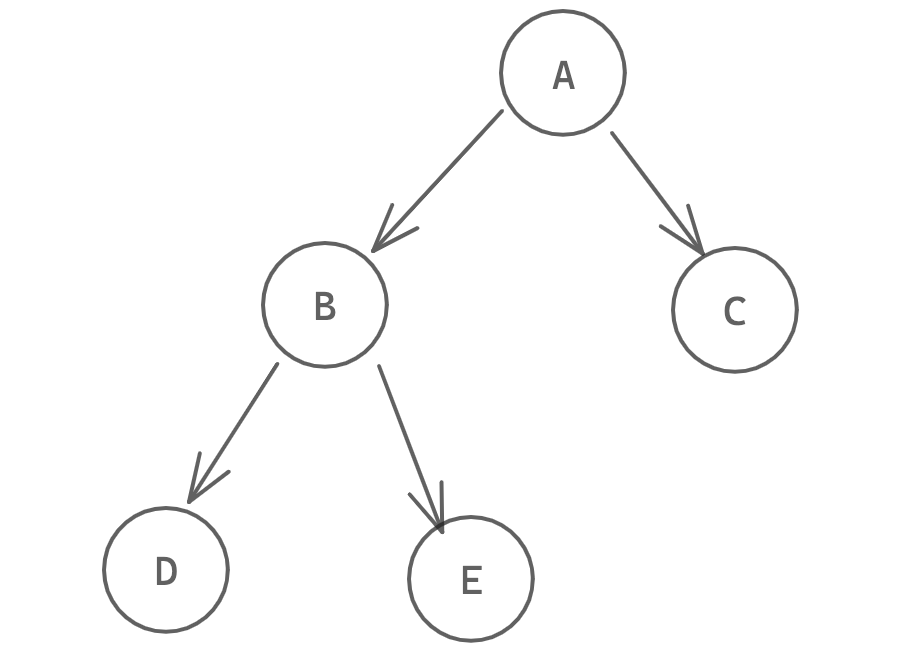
左边的子节点称为左孩子,右边的节点称为右孩子。二叉树就有比较多的性质了:
- 节点数量为
n,则边的数量为n-1 - 度为2的节点个数等于叶子节点个数-1,即$n_2=n_0 -1$
- 第
k层(k$\geq1$)有$2^k-1$个节点 - 节点
i(i$\geq 1$)的左儿子编号为$2\times i$ ,由儿子编号为 $ 2\times i+1$
有下面几种遍历顺序:
- 先序遍历
- 中序遍历
- 后序遍历
- 层序遍历
3 二叉搜素树
二叉搜索树的左孩子节点的值小于父节点的值,右孩子节点的值大于父节点的值。
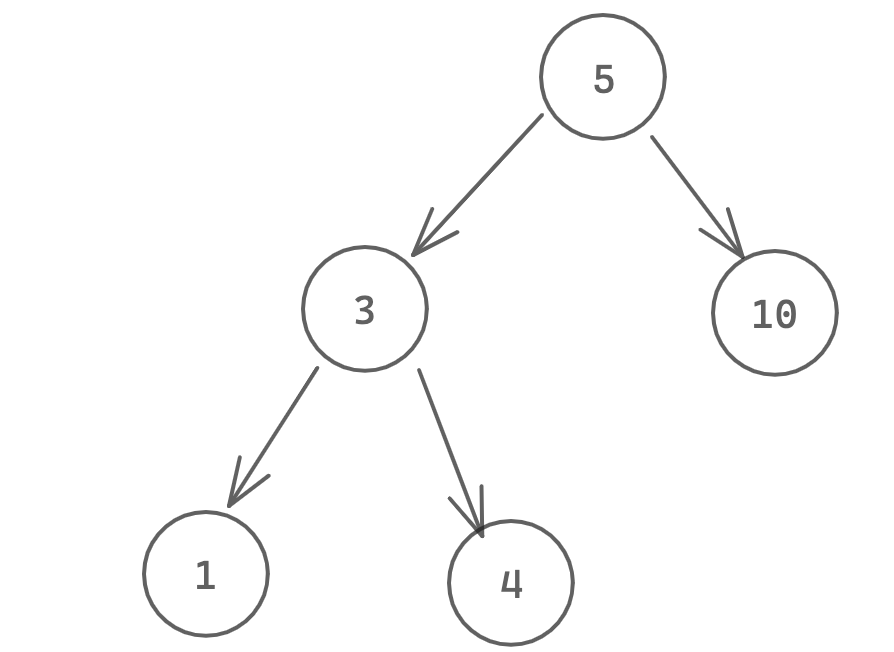
由于它具有这样的性质,因此查找一个在树上的值,可以使用到二分思想查找,时间复杂度为$O(log n)$,但是在极端情况下,即一条链的时候还是$O(n)$,因此有各种各样的平衡树来解决这个问题。
4 AVL树
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
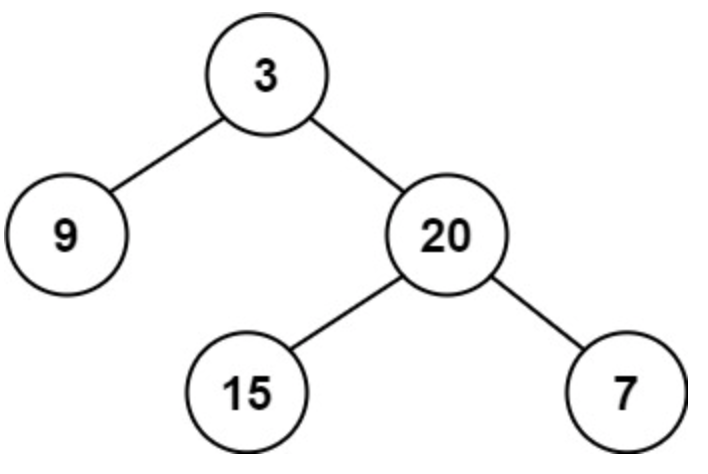
二叉树的平衡化有两大基础操作: 左旋和右旋。左旋,即是逆时针旋转;右旋,即是顺时针旋转。这种旋转在整个平衡化过程中可能进行一次或多次,这两种操作都是从失去平衡的最小子树根结点开始的(即离插入结点最近且平衡因子超过1的祖结点)。
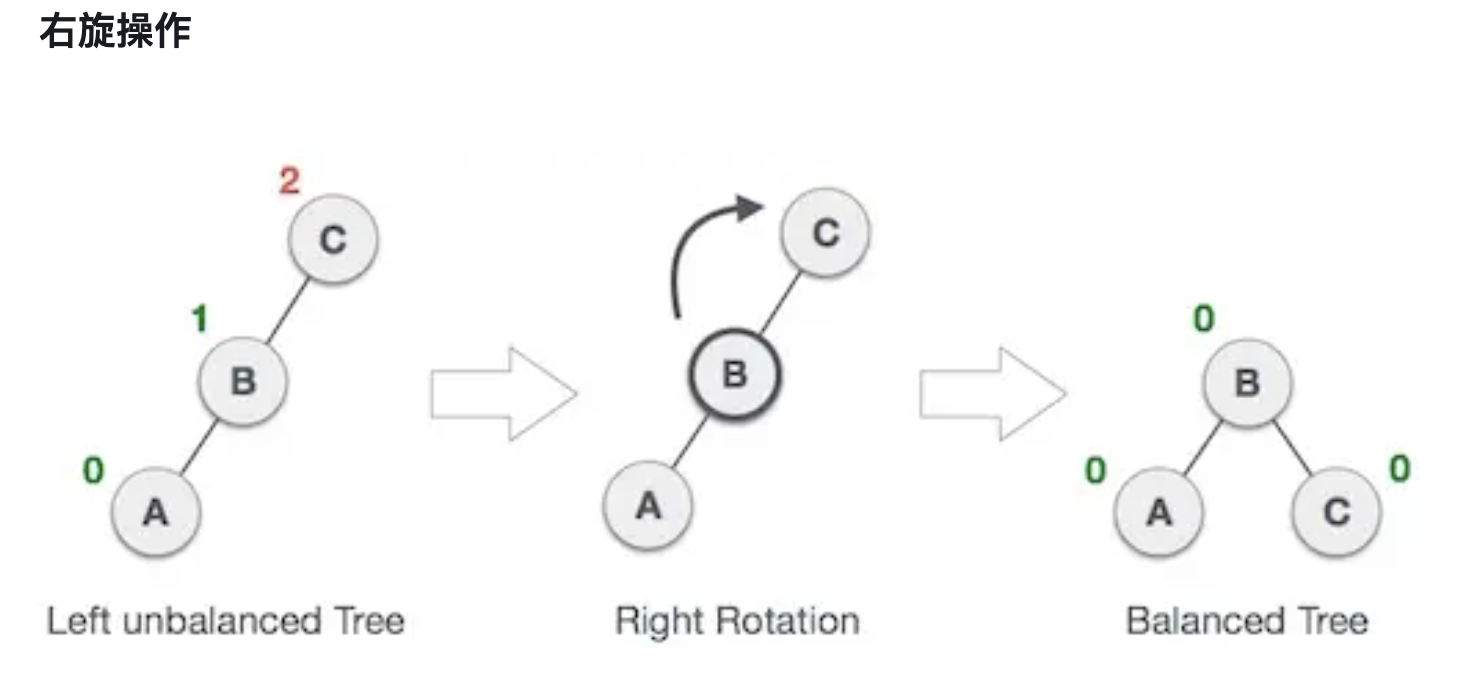
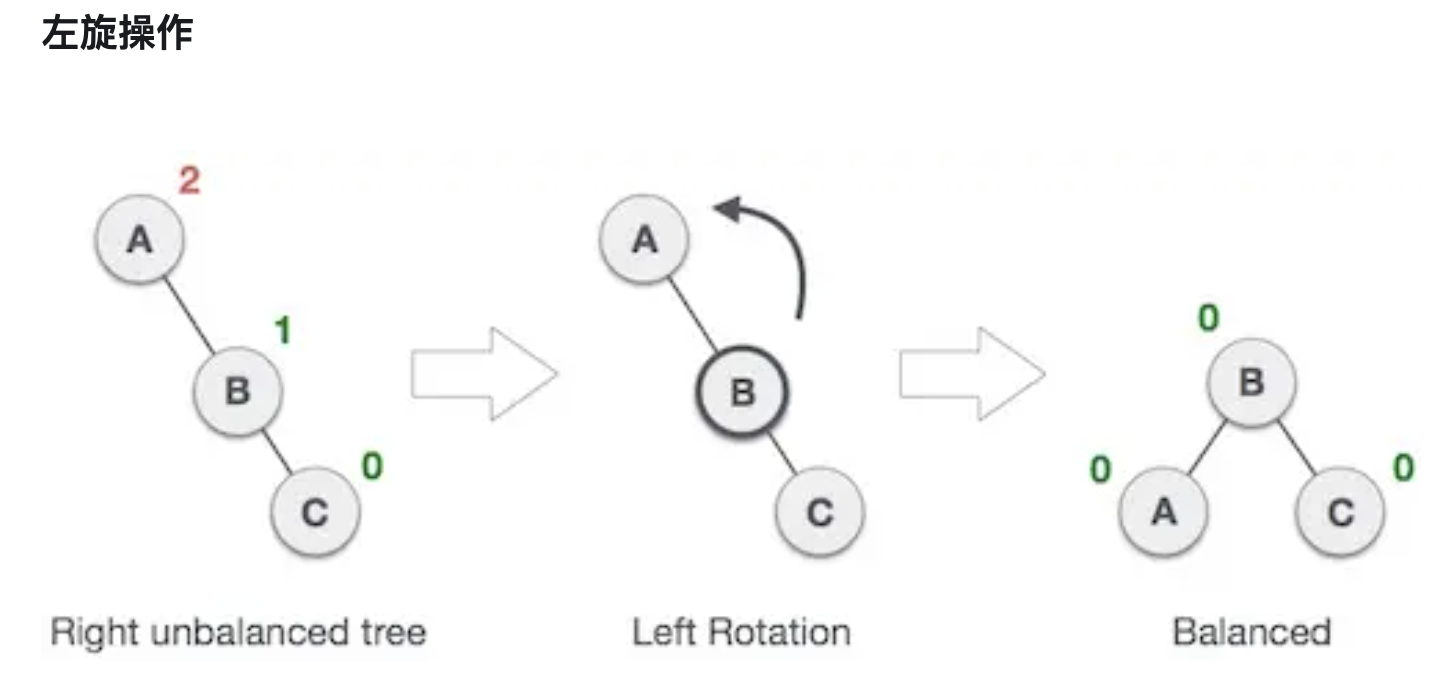
优点:适用于查询场景
缺点:容易频繁的调整,因此不适用于修改频繁的场景,这也是为什么红黑树用的多的原因。
5 红黑树
红黑树是一棵二叉搜索树,它在每个结点上增加了一个存储位来表示结点的颜色,可以是RED或BLACK。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确 保没有一条路径会比其他路径长出 2 倍,因而是近似平衡的。
红黑树的原则有以下几点:
- 特性1:节点非黑即红
- 特性2:根节点一定是黑色
- 特性3:叶子节点(NIL)一定是黑色
- 特性4:每个红色节点的两个子节点都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 特性5:从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点。
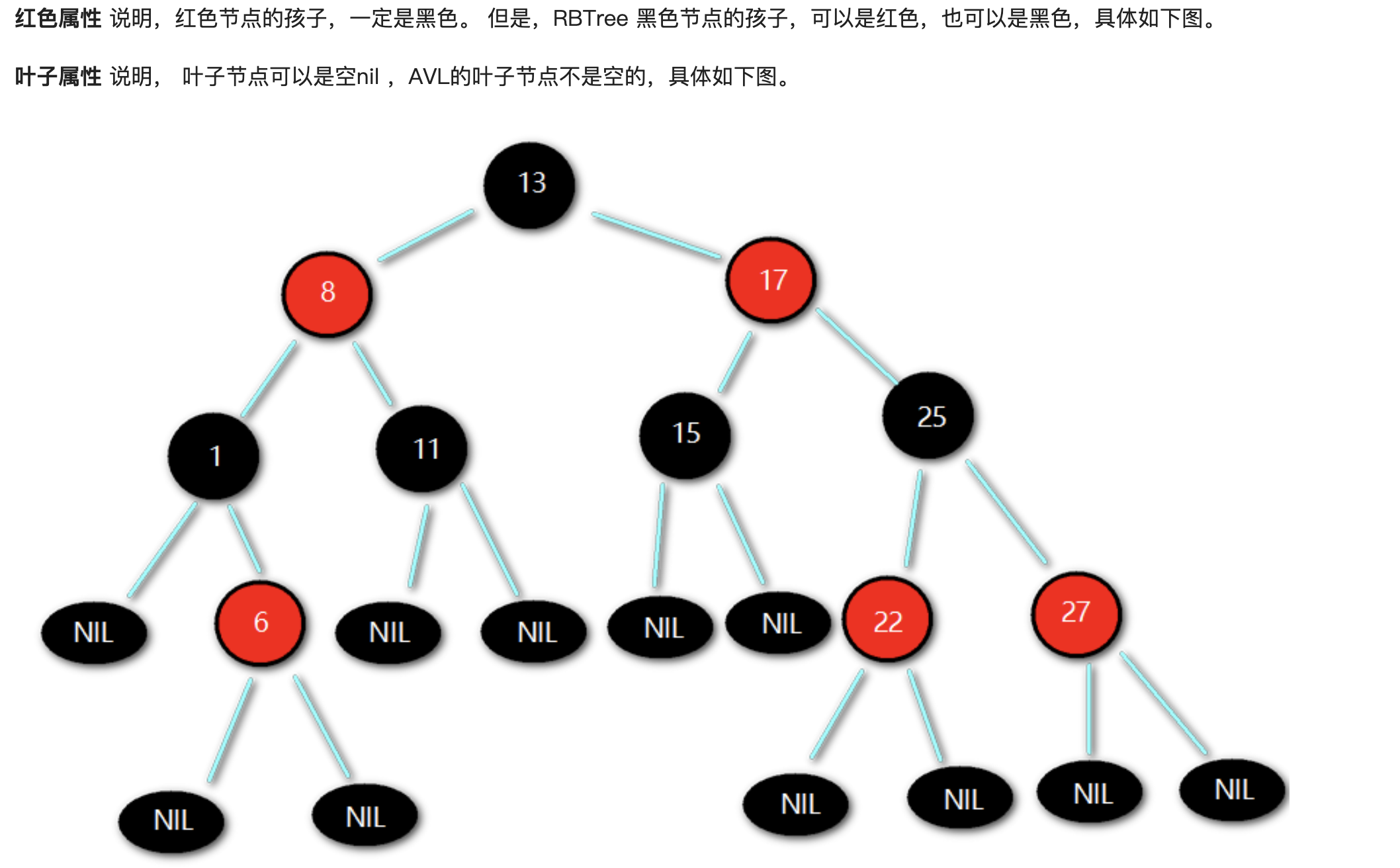
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 海岛一隅!
