trie前缀树

1 定义

Trie树，即字典树，又称前缀树，是一种树形结构，是一种哈希树的变种，像字典一样的树。

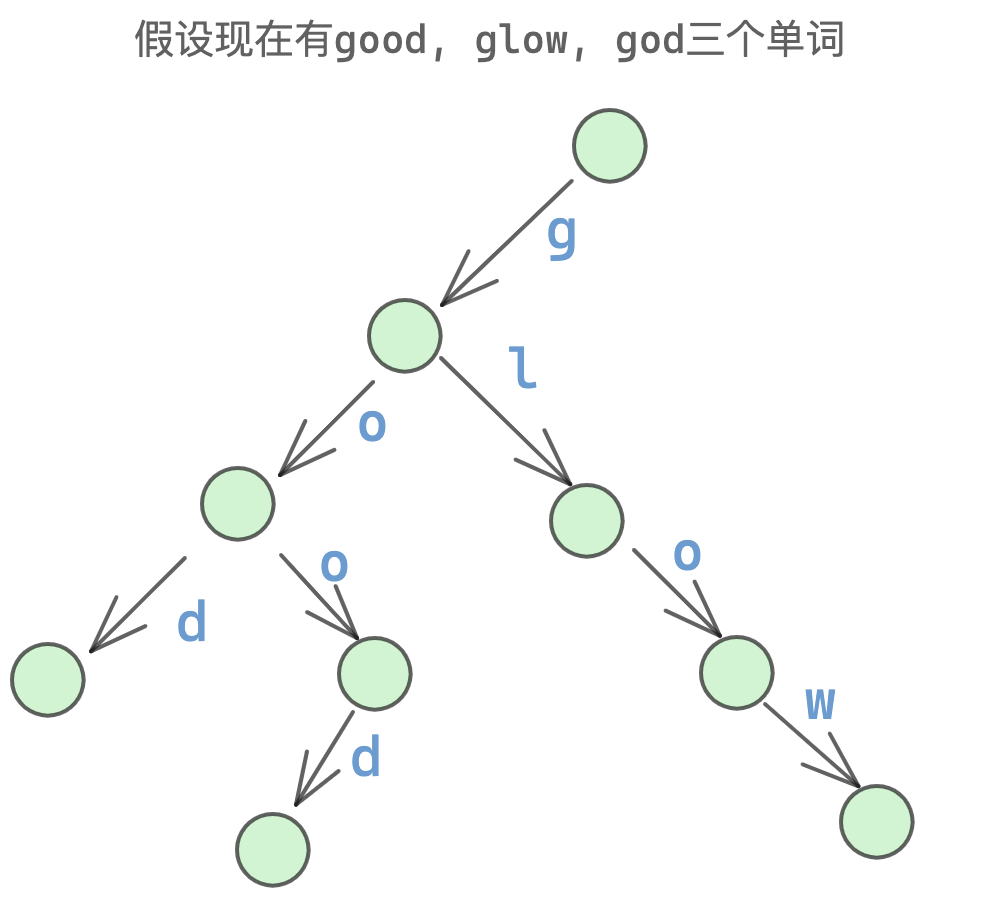
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的，使用Trie相比哈希查询的好处是，路由算法中需要模糊匹配，哈希是做不到的，它只能精确查找。

2 实现

2.1 字段

class Trie{
public:
    int tag;
    Trie *nxt[26]{};
    Trie(): tag(0) {}
};

首先定义核心字段，tag用来表示当前节点是否是某个字符串的结尾，比如说如果在上面的树中，又来了一个go，那在第一个o中的tag应该标识为1

2.2 插入

void insert(const string &s) {
    Trie *p = this;
    for (char i : s) {
        if (p->nxt[i - 'a'] == nullptr) {
            p->nxt[i - 'a'] = new Trie();
        }
        p = p->nxt[i - 'a'];
    }
    p->tag = 1;
}

• 如果子节点不存在，则新建一个子节点

• 移动p指针

• 将最后一个字符的tag置为1，标识一个字符串的末尾

2.3 查询

bool search(const string &s) {
    Trie *p = this;
    for (char i : s) {
        if (p->nxt[i - 'a'] == nullptr) {
            return false;
        }
        p = p->nxt[i - 'a'];
    }
    return p->tag;
}

• 如果遍历到子节点为nullptr，则直接返回false
• 移动p指针
• 判断最后一个p->tag是否为1

2.4 前缀匹配

bool startsWith(const string &prefix) {
    Trie *p = this;
    for(char i : prefix) {
        if(p->nxt[i-'a'] == nullptr)
            return false;
        p = p->nxt[i-'a'];
    }
    return true;
}

• 跟查询差不多

整个类的完整实现如下：

class Trie{
public:
    int tag;
    Trie *nxt[26]{};
    Trie(): tag(0) {}
    void insert(const string &s) {
        Trie *p = this;
        for (char i : s) {
            if (p->nxt[i - 'a'] == nullptr) {
                p->nxt[i - 'a'] = new Trie();
            }
            p = p->nxt[i - 'a'];
        }
        p->tag = 1;
    }
    bool search(const string &s) {
        Trie *p = this;
        for (char i : s) {
            if (p->nxt[i - 'a'] == nullptr) {
                return false;
            }
            p = p->nxt[i - 'a'];
        }
        return p->tag;
    }

    bool startsWith(const string &prefix) {
        Trie *p = this;
        for(char i : prefix) {
            if(p->nxt[i-'a'] == nullptr)
                return false;
            p = p->nxt[i-'a'];
        }
        return true;
    }
};

下面提供一个go实现的版本

type Trie struct {
    nxt [26]*Trie
    tag int
}

func (this *Trie) Insert(word string) {
    root := this
    for _, c := range word {
        if root.nxt[c-'a'] == nil {
            root.nxt[c-'a'] = &Trie{}
        }
        root = root.nxt[c-'a']
    }
    root.tag = 1
}

func (this *Trie) Search(word string) bool {
    root := this
    for _, c := range word {
        if root.nxt[c-'a'] == nil {
            return false
        }
        root = root.nxt[c-'a']
    }
    return root.tag == 1
}

func (this *Trie) StartsWith(prefix string) bool {
    root := this
    for _, c := range prefix {
        if root.nxt[c-'a'] == nil {
            return false
        }
        root = root.nxt[c-'a']
    }
    return true
}

想要做题的话可以去试试这个 leetcode 208. 实现 Trie (前缀树)

3 radix tree

gin框架并不是使用普通的trie树，而是一种经过压缩的Radix Trie又叫做基数树、基数特里树、压缩前缀树。

当某个父节点仅有一个子节点，并且不存在字符串以该父节点为结尾的时候，会将父节点和子节点进行合并，则最前面的trie树就会变成下图：

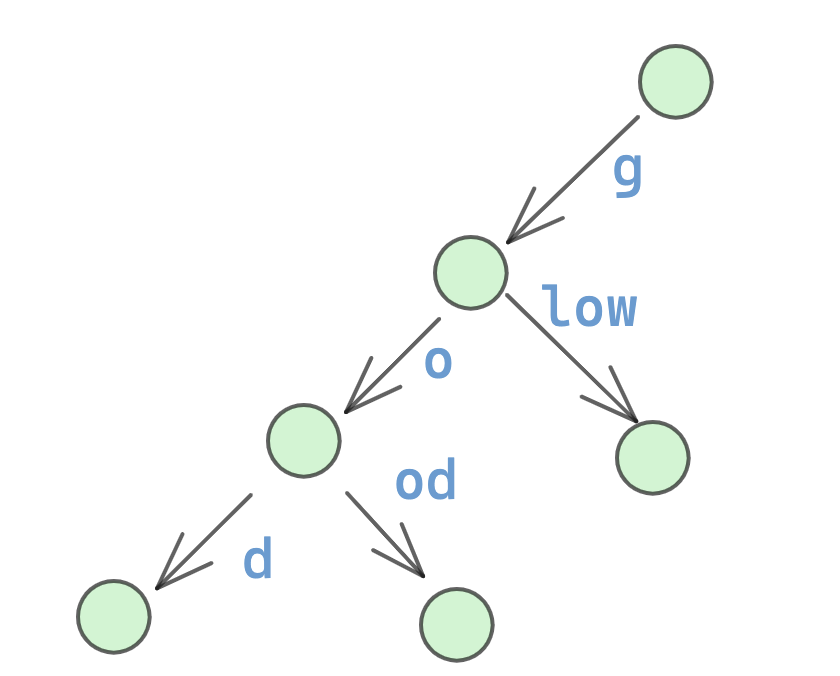
Reference:

HTTP Router 算法演进